阅读需知:本文从作者主观意见出发,如有不合适的地方,如:文章内容错误、文章排版混乱、逻辑思维混乱,请第一时间在文章评论区留言。
今天👴来写PHP反序列化漏洞,PHP作为👴认为的(世界上最好的语言),必定存在着世界上最好的漏洞
阅读需知:本文从作者主观意见出发,如有不合适的地方,如:文章内容错误、文章排版混乱、逻辑思维混乱,请第一时间在文章评论区留言。
今天👴来写PHP反序列化漏洞,PHP作为👴认为的(世界上最好的语言),必定存在着世界上最好的漏洞
Forest in an easy difficulty Windows Domain Controller (DC), for a domain in which Exchange Server has been installed. The DC is found to allow anonymous LDAP binds, which is used to enumerate domain objects. The password for a service account with Kerberos pre-authentication disabled can be cracked to gain a foothold. The service account is found to be a member of the Account Operators group, which can be used to add users to privileged Exchange groups. The Exchange group membership is leveraged to gain DCSync privileges on the domain and dump the NTLM hashes.
很早就想重整一下农村家里的网络,毕竟服务器和种种设备(监控、硬碟机、交换机…)都在家里,年初做了一版,简单画了张拓扑,可惜那时候整的不怎么样(资金不足、设备损坏等等原因),现在资金够了,该买的也买了,就随便写写吧。
栈是一种只能从表的一端存取数据且遵循 “先进后出”/“后进先出 (Last in First Out) “ 原则的线性存储结构,主要操作有入栈(push)和出栈(pop),往上叫栈顶,往下叫栈底
 栈
栈
在汇编中栈入栈和出栈的操作形式,先从ESP/RSP/SP寄存器(栈指针)指向的内存中读取数据写入其他内存地址或者基础,再根据不同的系统架构将栈指针的数值增加4(32位)或者增加8(64位)
买之前一直在罗兰FP30X和雅马哈P128之间徘徊,最终选择了雅马哈P125,希望这是一个不会让我后悔的选择。
产品价格:看官网价格,P-125 - 概述 - 可攜式數位鋼琴(P系列) - 鋼琴 - 樂器 - 產品 - Yamaha - 台灣
产品规格:P125B本体+U架+单踏(延音踏板)+礼包(转接头)
重量:提着爬六楼累得半死
在此之前我已经有了一台电子琴,注意是电子琴(带打击音效+编曲功能的那种),陪了我8年多,牌子叫(SHUSIAMAN,杂牌),记得当时到SM买的,花了3k多还送了个家教😅,学了两个月左右打下了基础(指基础指法,但这破电子琴只有61键,很难受),后来因为学业和种种原因就搁在那儿不动了,也就偶尔拿出来练个599,另外这台琴琴键是镂空的,不像传统钢琴一样中间是实心的,有到琴行和学校钢琴间摸过真钢,那手感真的不能比。。。
本篇文章仅列出一些易错点及小TIP,还有一些速记技巧(供那些临时抱佛脚的人使用),更深入的内容请自行了解。本人是在福建省考的试,各省份考试方式及费用可能略有不同,请翻阅自己省工信部网站上有关无线电的资料
题目已经熟透不少了,现在上场的话99.9%能拿满分,A类考试题目一共371道题,考试会从题库里边抽出30道题目来,总的来说还算简单,CRAC官网有配套的考试系统,测了几下都能满分,A类和B类题目都差不多,等考完A类后我就开始奋斗B类啦,争取六个月后顺利通过B类。
题目不怎么难,有初中物理基础基本上就能对一半,还有那本小绿皮(现在是小蓝皮?)写得很详细,整本看完基本上稳了。
步入正题,我花了几天刷A类题库,稍微总结了一下,A类40%政策题,60%技术题(大概是这样)
Modern Tetris tutorial for noobs
中文:新人如何入坑俄罗斯方块
【2022/8/14】看这里(TETRiS TRAiNER TRÈS-BiEN (teatube.cn))比我写的详细多了
打块这件事儿,人人都能学会。
菜的不能再菜的账号:Jstris | po7mn1 (jezevec10.com)
Telegram: @t.me/icecliffs(一起打块吧!)
整个烂活
先来回顾一下IP地址,这里只列出三种常用的IP地址,ABC类,IP地址由32个二进制组成。点分十进制表达法为:192.168.0.1
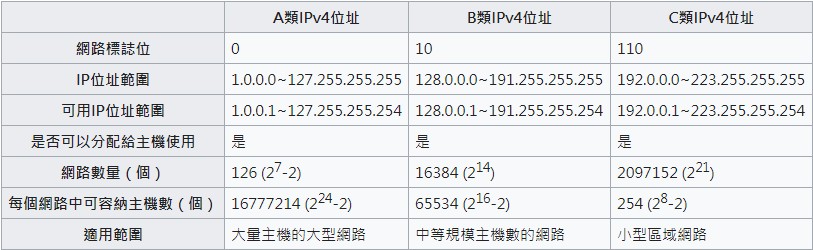
子网掩码的表示方法: