(70%) 408 Computer Data Structures

Research

第1章 绪论

常见复杂度排序：$O(1)<O(log_2n)<O(n)<O(nlog_2n)<O(n^2)<O(n!)<O(n^n)$

时间复杂度：常规的直接数一下暴力，循环最好想一下展开的量级关系

第2章 线性表

线性表示一种逻辑结构

顺序表

随机查找、顺序存储形式。

分配（动态）：L.data = (ElemType *)malloc(sizeof(ElemType)*InitSize);

链表

非随机读取，不支持随机查找、链式存储结构，节点空间可以动态申请和释放。

单链表

1
2
3
4
typedef struct LNode {
    ElemType data;
    struct LNode *next;
} LNode, *LinkList;

双链表

1
2
3
4
typedef struct DNode {
    ElemType data;
    struct DNode *prior, *next;
} DNode, *DLinkList;

操作

插入（头插法单链表）

1
2
3
4
LNode *s = (LNode *)malloc(sizeof(LNode));
s->data = x;
s->next = L->next;
L->next = s;

插入（尾插法单链表）

1
2
3
4
LNode *s = (LNode *)malloc(sizeof(LNode));
s->data.= x;
r->next = s;
r = s; // 这里指向了新的表尾节点

双链表插入（p结点之后插入s）

1
2
3
4
s->next = p->next;
p->next->prior = s;
s->prior = p;
p->next = s;

几个时间复杂度

顺序表

  • 插入：表尾 $O(1)$、表头 $O(n)$
  • 删除：平均为 $O(n)$
  • 查找：$O(n)$

第3章 栈、队列和数组

栈

先进后出（FILO）、后进先出（LIFO）

顺序栈

动态顺序栈，动态一维数组来存储

1
2
3
4
5
6
#define Stacksize 50
typedef int ElemType;
typedef struct Sqstack {
  ElemType *bottom, *top;
  int Stacksize;
} Sqstack, *SqStack;

静态顺序栈

1
2
3
4
5
6
#define MaxSize 50
typedef int ElemType;
typedef struct Sqstack {
  ElemType data[MaxSize];
  int top;
} Sqstack, *SqStack;

入栈：先进指针，再进入元素 ++(S.top); S.data[S.top] = x;

共享栈

两个栈共享同一片内存空间，两个栈从两边往中间增长

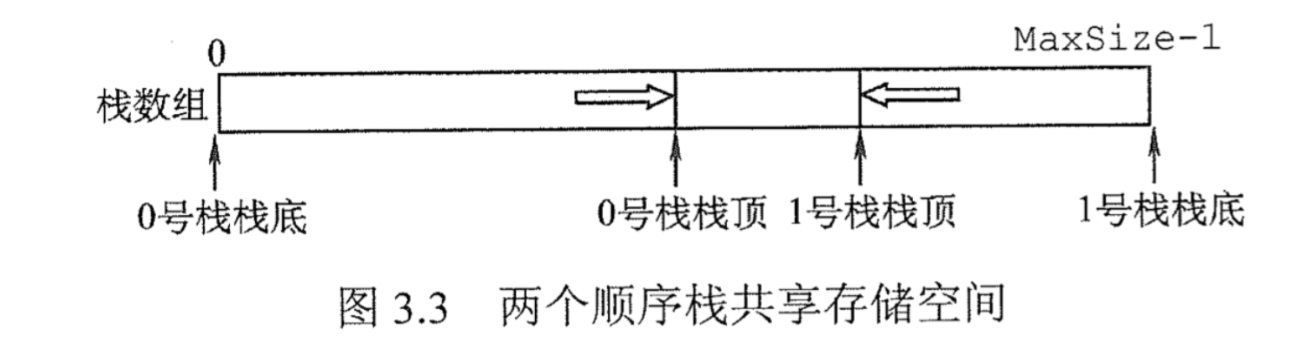
image-20250802202045507

链栈

1
2
3
4
typedef struct LNode {
  ElemType data;
  struct LNode *next;
} LNode;

入栈头插法、出栈头出法。

便于多个栈共享存储空间，提高效率，且不存在上溢的现象

进栈操作

1
2
3
4
5
p=(LNode *)malloc(sizeof(LNode));
p->next=NULL;
p->data=x;
p->next=lst->next;
lst->next=p->next;

出栈操作，头结点后面的结点删除

1
2
3
4
p=lst->next;
x=p->data;
lst->next=p->next;
free(p);

栈的应用

括号匹配

表达式求值

递归

队列

顺序队列

重点：先进先出（FIFO）

顺序实现

1
2
3
4
5
#define MaxSize 10
typedef struct {
  ElemType data[MaxSize];
  int front, rear;
} SqQueue;

循环队列入队取模

1
2
3
4
5
6
7
bool EnQueue(SqQueue &Q, ElemType x) {
  if ((Q.rear+1) % MaxSize == Q.front)
    return false;
  Q.data[Q.rear] = x;
  Q.rear(Q.rear+1)%MaxSize;
  return true;
}

双端队列

两边都可以灌满，分为前端后端都可以入队和出队

链队

头出尾插的单链表

1
2
3
4
5
6
7
typedef struct {
  ElemType data;
  struct LinkNode *next;
} LinkNode;
typedef struct {
  LinkNode *front, *rear;
} LinkQueue;

多维数组

第4章 串

KMP算法

主要用于匹配字符串，看代码理解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int KMP(string &S, string &P, int next[]) {
  int i = 1, j = 1; // 索引
  while (i <= S,length()) {
    if (j == 0 || S[i] == P[j]) {
      ++i; ++j;
    } else {
      j = next[j]; // 根据 next 数组，回退模式串索引
    }
    if (j > P.length()) {
      return i - P.length();
    }
  }
  return 0;
}

第5章 树与二叉树

基本概念

常考性质

结点数=总度数+1
高度为h的m叉树至多有$\frac{m^h-1}{m-1}$个节点

image-20250802202000955

具有n个结点的m叉树的最小高度为$log_m(n(m-1)+1)$

二叉树

注意区别：度位2的有序树

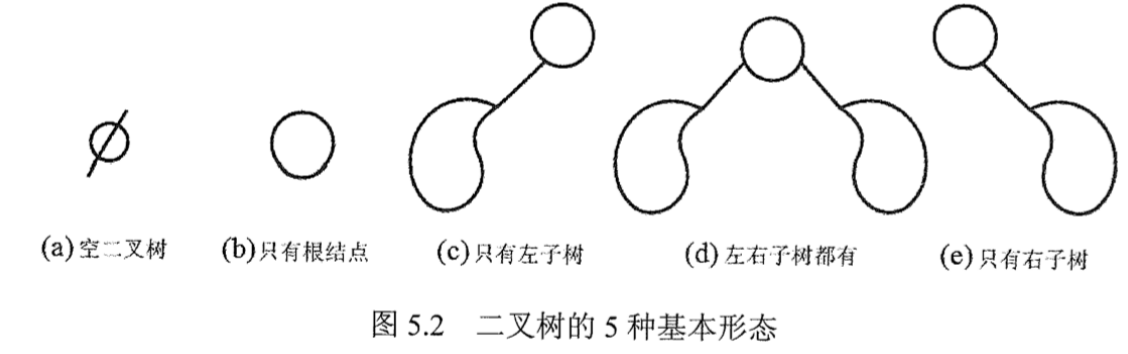
image-20250806143221629

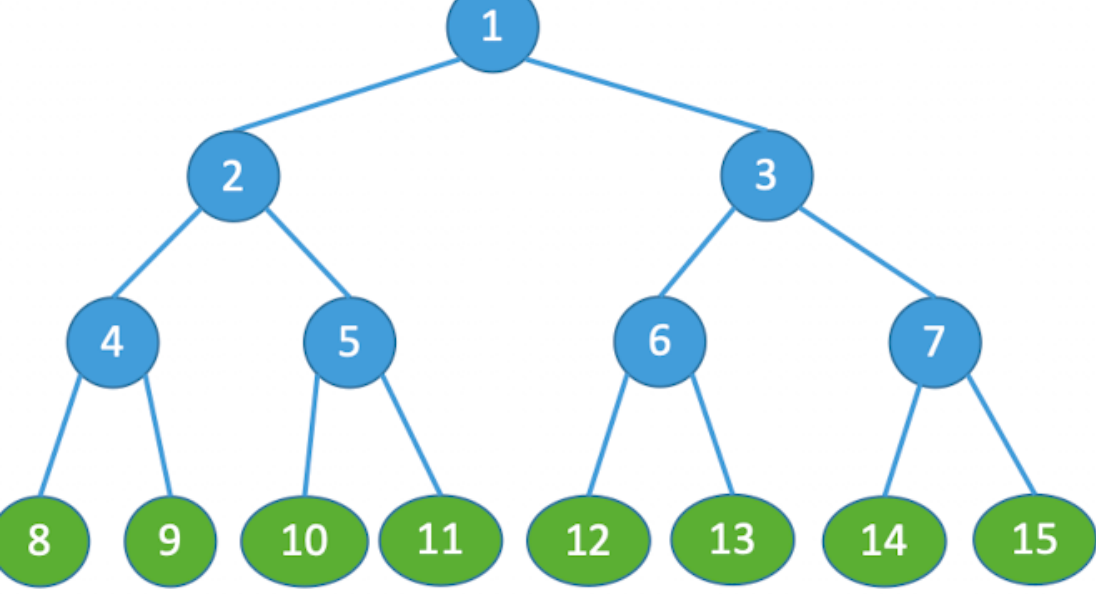
满二叉树

一棵高度为 $h$，且含有 $2^h-1$ 个结点的二叉树

image-20250802202302638

image-20250806143254648

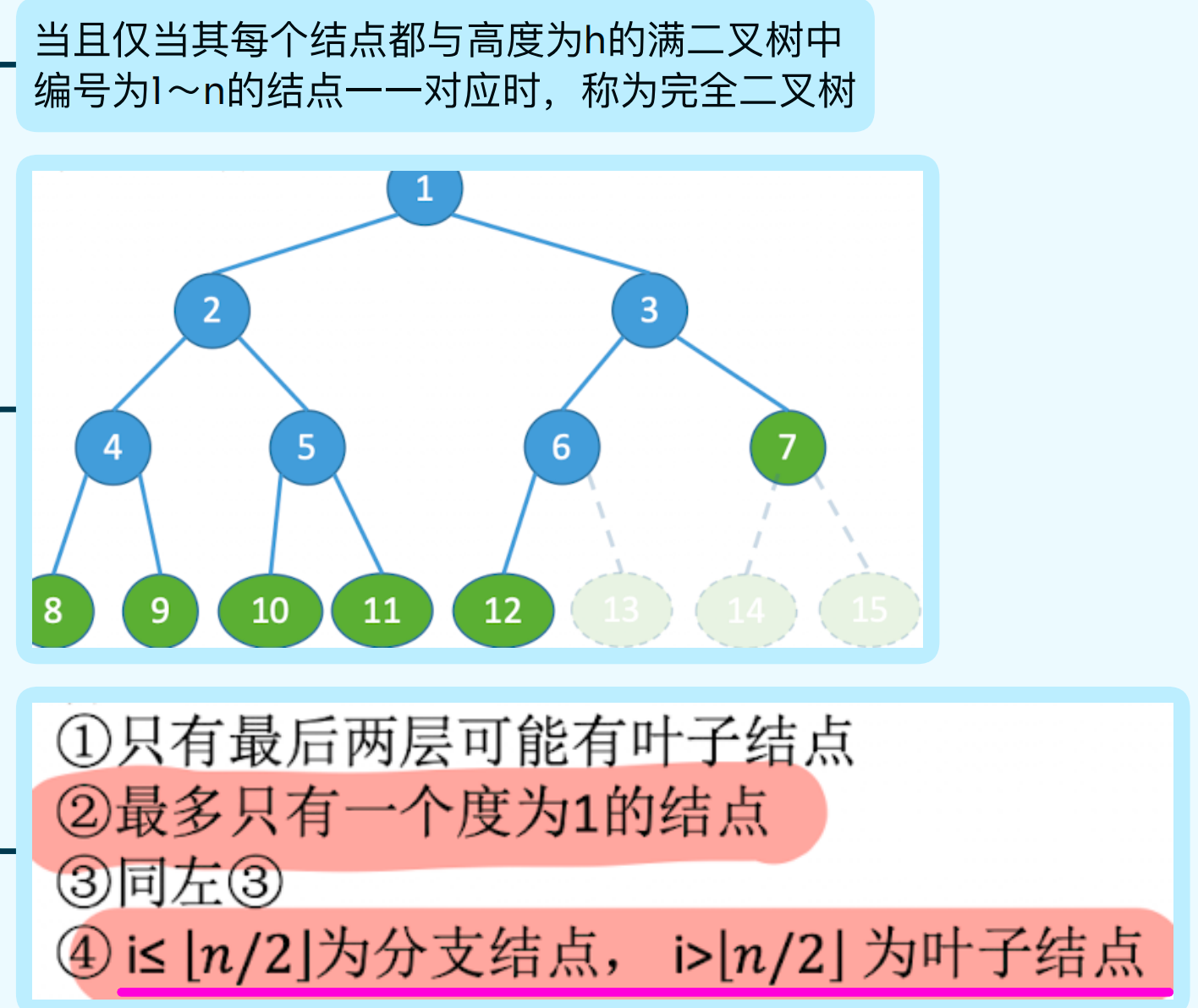
完全二叉树

image-20250806143308192

二叉排序树（BST）

二叉排序树。一棵二叉树或者空二叉树，或者是具有如下性质的二叉树：

  • 左子树上所有节点的关键字均小于根节点的关键字
  • 右子树上所有节点的关键字均大于根节点的关键字

平衡二叉树（AVL）

树上任一结点的左子树和右子树的深度之差不超过1的排序树

二叉树第i层至多有$2^{i-1}$个结点（i>=1）

高度为h的二叉树至多有$2^h-1$个结点（满二叉树，至少h个）

树的存储

用一组地址连续存储单元依次自上而下、自左而右存储完全二叉树上的元素

顺序存储

只适用于满二叉树和完全二叉树

  • i的左孩子，2i
  • i的右孩子，2i+1
  • i的父节点，[i/2]

链式存储

n个结点的二叉链表共有n+1个空链域，空指针域可用于后面构造线索二叉树

1
2
3
4
5
6
// 二叉树的结点
typedef struct BiTNode {
  ElemType data;
  struct BiTNode *lchild, *rchild;
  struct BiTNode *parent; // 三叉链表，方便找到父结点
} BiTNode, *BiTree;

二叉树遍历

先/中/后序遍历

代码实现都是迭代，空间复杂度为 $O(h)$

先序：根左右（NLR）

1
2
3
visit(p);
preorder(p->lchild);
preorder(p->rchild);

中序：左根右（LNR）
后序：左右根（LRN）

也可以用递归（栈），求遍历序列

层序遍历

用队列

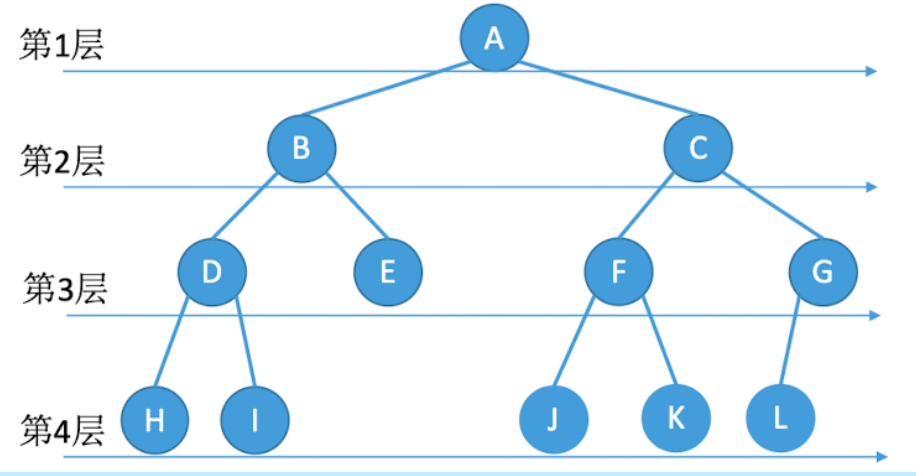
image-20250806200128623

由遍历序列构造二叉树

如果给出一棵二叉树的前/中/后/层序遍历序列中的一种，则不能确定唯一一棵二叉树

关键：找到树的根节点，并根据中序序列划分左右子树，在找到左右子树的根节点

可以唯一确定的二叉树
前序+中序
后序+中序
层序+中序

线索二叉树

允许通过线索在树的节点之间移动，而不是通过正常的分支来移动，标志域、目的、线索（指向结点前驱 or 后继的指针）、线索化

1
2
3
4
5
typedef struct ThreadNode {
  ElemType data;
  struct ThreadNode *lchild, *rchild;
  int ltag, rtag; // 新增的左右线索标志
} ThreadNode, *ThreadTree;

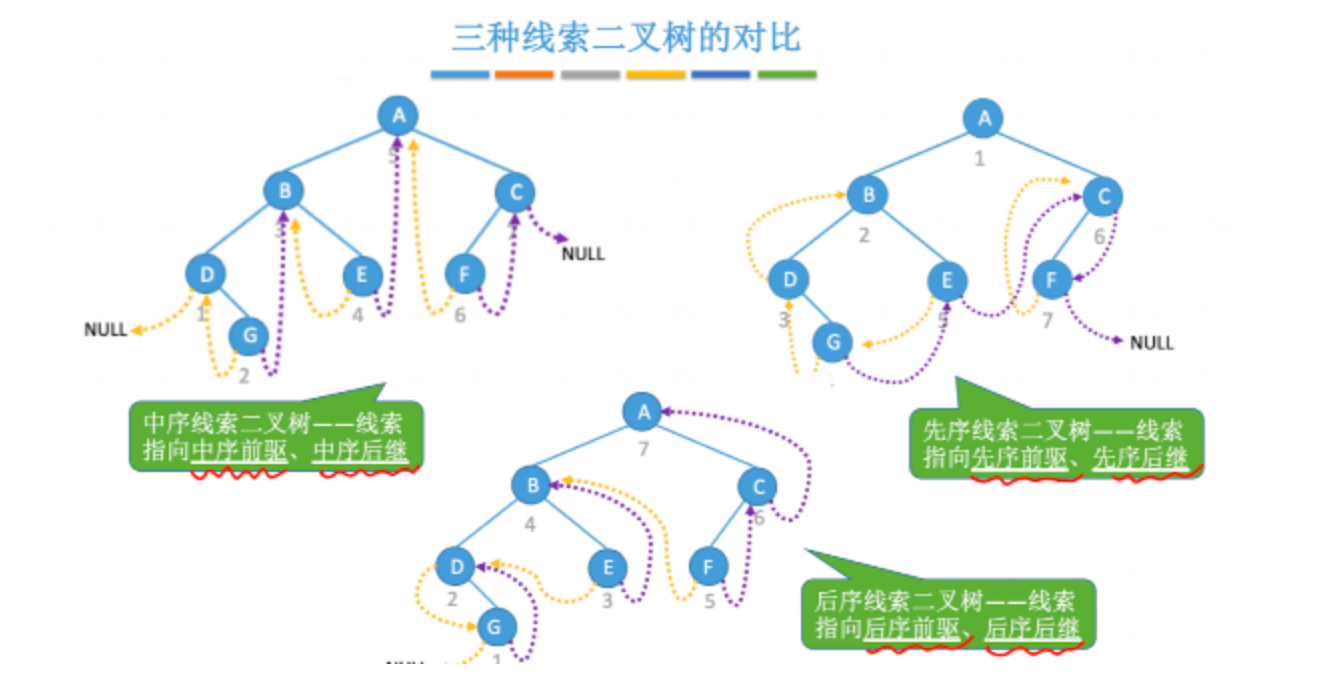
image-20250825142917921

黄色代表前驱，紫色代表后继
前驱和后继

  • 中序前驱、中序后继
  • 先序前驱、先序后继
  • 后序前驱、后序后继

二叉排序树（BST）

又称二叉查找树，定义 左子树结点值<根结点值<右子树结点值

BST的查找

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// 结构
typedef structure BSTNode {
  int key;
  struct BSTNode *lchild, *rchild;
} BSTNode, *BSTree;
// 在二叉排序树中查找值为key的结点
BSTNode *BST_Search(BSTree T, int key) {
  while (T!=NULL&&key!=T->key) { // 若树为空或等于根节点值，则跳出循环
    if (key<T->key) {
      T=T->lchild; // 小于，则在左子树上查找
    } else {
      T=T->rchild; // 大于，则在右子树上查找
    }
  }
}

平衡二叉树（BBT｜AVL）

树上任意结点的左子树和右子树的高度之差不超过1，平衡二叉树有BST的特点：左<根<右

1
2
3
4
5
6
// 平衡二叉树结点
typedef structure AVLNode {
  int key; // 数据域
  int balance; // 平衡因子
  struct AVLNode *lchild, *rchild;
} AVLNode, *AVLTree;

调整不平衡二叉树

LL平衡旋转（右单旋转）

由于结点A的左孩子L的左子树L插入新结点导致不平衡

RR平衡旋转（左单旋转）

由于结点A的右孩子R的右子树R插入新结点导致不平衡

LR平衡旋转（先左右后双旋转）

由于结点A的左孩子L的右子树R插入新结点导致不平衡

RL平衡旋转（先右后左双旋转）

由于结点A的右孩子R的左子树L插入新结点导致不平衡

应用

哈夫曼树和哈夫曼编码

哈夫曼树

定义：带权路径长度最小的二叉树

树的带权路径长度WPL：
$$
WPL=\sum^{n}_{i=1}w_il_i
$$

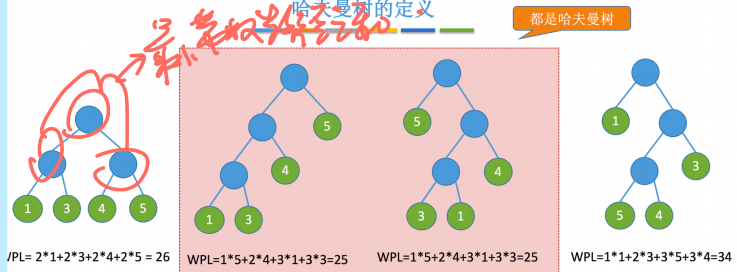
image-20250826164737029

构造方法：

  1. 每个初始结点最终成为叶子结点，且权值越小的结点到根节点的路径长度越大
  2. 哈夫曼树的节点总数为 $2n-1$
  3. 哈夫曼树中不存在度为1的结点
  4. 哈夫曼树并不为一，但WPL必然相同为最优

哈夫曼编码

编码分为固定长度编码（每个字符用相等长度的二进制表示）和可变长度编码（允许对不同字符用不等长的二进制位表示）

前缀编码：若没有一个编码是另外一个编码的前缀，则称这样的编码为前缀编码。

哈夫曼编码：由哈夫曼树得到哈夫曼编码，字符集中的每个字符为一个叶子结点，各个字符出现的频度作为结点的权值

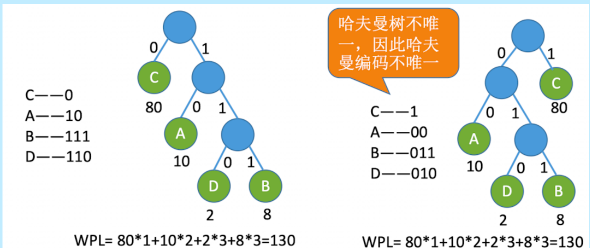
image-20250826165830169

应用用途为：数据压缩，例如JPEG图像

第6章 图

有向图

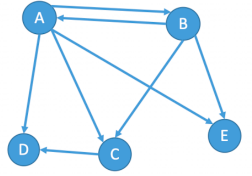
若E是有向边（弧）的有限集合时，则图G为有向图，有弧头弧尾，具体看下面，解释说明

有向图G；弧<v,w>，v弧头、弧尾，从顶点v到顶点w的弧；
$$
G_1=(V_1,E_1)\\
V_1={A,B,C,D,E}\\
E_1={<A,B>,<A,C>,<A,D>,<A,E>,<B,A>,<B,C>,<B,E>,<C,D>}
$$
image-20250826170353152

无向图

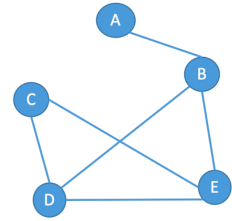
若E是无向边（边）的有限集合时，则图G为无向图，边是顶点的无序对，记为(v,w)或(w,v)，因为**(v,w)=(w,v)**
$$
G_2=(V_2,E_2)\\
V_2={A,B,C,D,E}\\
E_2={(A,B),(B,D),(B,E),(C,D),(C,E),(D,E)}
$$
image-20250826170839691

简单图

条件：图中不存在重复边，不存在定点到自身的边

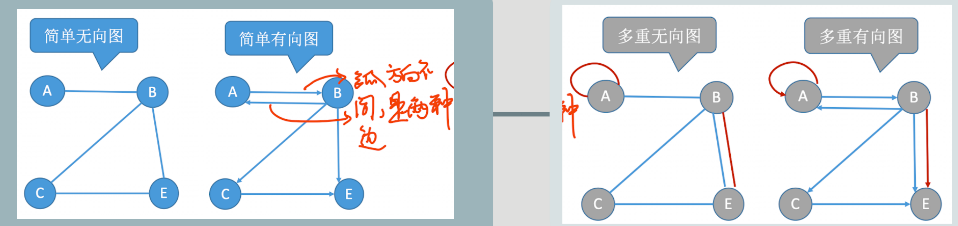
image-20250826174034238

多重图

条件：若图G中某两个定点之间的变数大于一条，又允许顶点通过一条边和自身相关联

完全图

完全图（简单完全图）：对于无向图，|E|的取值范围为0到$\frac{n(n-1)}{2}$，有$\frac{n(n-1)}{2}$条边的无向图称为完全图，完全图中，任意两个顶点之间都存在边，对有向图，在有向完全图中任意两个顶点之间都存在方向相反的两条弧

图的存储

邻接矩阵法

邻接表法

十字链表法（有向图）

邻接多重表（无向图）

图的遍历

广度优先遍历（BFS）

深度优先遍历（DFS）

图的应用

最小生成树

最短路径

Dijkstra迪杰斯特拉算法

Floyd弗洛伊德算法

第7章 查找

第8章 排序